La serie TV Il problema dei 3 corpi di Netflix sta affascinando il pubblico mondiale anche a livello intellettuale, visto che lo show basato sulla saga letteraria fantascientifica “Memoria del passato della Terra” pone, al pari dell’opera letteraria dell’autore cinese Liu Cixin, le sue fondamenta su concetti e conoscenze scientifiche non certo alla portata di tutti. Ecco, dunque, che in tanti hanno cominciato a chiedersi cos’è davvero il problema dei tre corpi nella fisica, oppure cos’è il cosiddetto paradosso di Fermi, argomenti che stanno incuriosendo sempre più persone.
Con questo articolo, tutt’altro che supponente, guidati principalmente dalla nostra passione tutta nerd per la scienza e la fisica, cercheremo di descrivere in maniera semplice ma razionale cos’è il problema dei tre corpi, partendo da ciò che viene narrato nella serie TV di Netflix firmata dagli autori di Game of Thrones.
Sinossi de Il problema dei 3 corpi
Nello show un’avanzata civiltà aliena sviluppatasi su un pianeta che si trova in un sistema a tre stelle, è costretta a cercare una nuova casa per via della futura distruzione del pianeta Trisolaris proprio perché facente parte di un sistema planetario con tre soli, quindi instabile. Riducendo così ai minimi termini la sinossi della serie TV ed evitando spoiler, capiamo subito perché il titolo dello show (e dunque del primo libro della trilogia sci-fi di Cixin) sia legato proprio al problema dei tre corpi.
La fisica del problema dei tre corpi
Immaginate una mite sera d’estate nell’antica Grecia… scusate, la sheldonite da The Big Bang Theory si stava impadronendo di me.
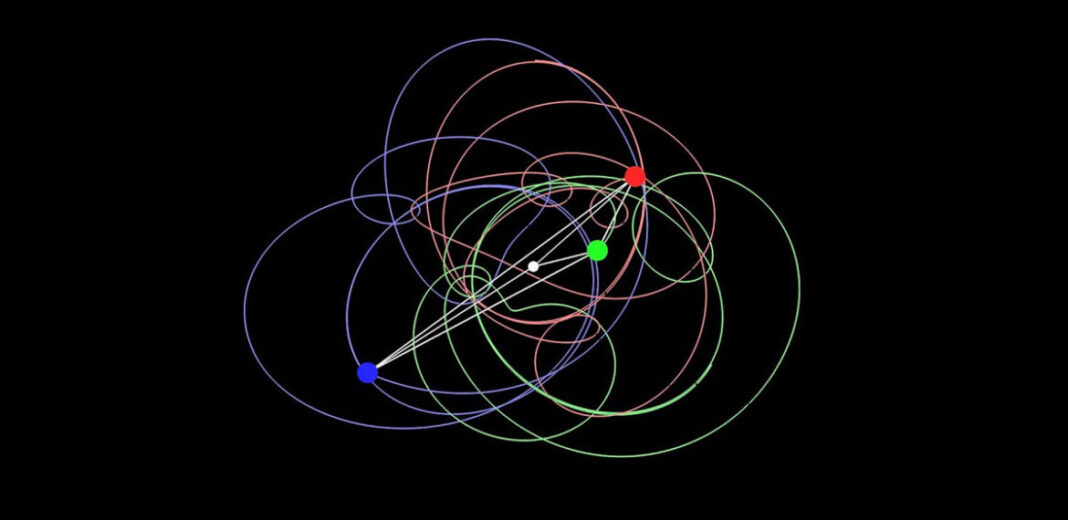
Torniamo seri e razionali e partiamo dalla definizione: il problema dei tre corpi è una classe di problemi della dinamica riferita alla meccanica classica che riguarda l’impossibilità di calcolare con estrema esattezza l’evoluzione di un sistema costituito da tre corpi soggetti alla reciproca attrazione gravitazionale, conoscendo come dati iniziali la loro posizione, la loro massa e la loro velocità.
Grazie a Galileo, Keplero e Newton sappiamo da secoli che la Terra orbita attorno al Sole seguendo un percorso ellittico in cui la nostra stella occupa uno dei due fuochi, obbedendo alla Legge di Gravitazione Universale formulata nel 1687 proprio da Isaac Newton.
Per la legge di gravitazione universale due corpi si attraggono in maniera direttamente proporzionale alle loro masse e inversamente proporzionale al quadrato della loro distanza, equazione che, dunque, descrive e risolve il problema dei due corpi. Tuttavia, quando si tenta di estendere questo modello matematico tre o più corpi, le complicazioni aumentavano esponenzialmente e il comportamento di questi corpi diventa imprevedibile e difficilmente rappresentabile in modo semplice.
I tre corpi: un problema insormontabile anche per Isaac Newton
Lo stesso Newton non riuscì a trovare una soluzione al problema dei tre corpi, un’equazione che fosse in grado di descrivere il sistema e prevedere il suo sviluppo nel tempo, calcolando velocità e posizione dei corpi celesti coinvolti.
Uno dei principali ostacoli nel risolvere questo problema è la sua non linearità.
In un sistema a due corpi, come quello formato dal Sole e dalla Terra oppure dalla Terra e dalla Luna, le equazioni differenziali che descrivono il loro moto possono essere risolte analiticamente. Con tre o più corpi, però, l’interazione gravitazionale tra di essi genera una serie di effetti che non possono essere facilmente previsti.
Un problema senza soluzioni… forse
Nel 1892 il matematico francese Henri Poincaré dimostrò che non esiste alcuna soluzione matematica la problema dei tre corpi, aspetto che nella serie TV viene sottolineato più volte quando alcuni giocatori del videogame presente nello show affermano di poter prevedere con esattezza l’alternarsi dell’ere del caos.
Eppure, l’umanità è riuscita nel corso della sua evoluzione a scoprire pian piano i segreti dell’universo e le leggi che lo regolano, permettendoci di lanciare sonde nello spazio, pianificare e prevedere le loro orbite attorno ai pianeti del sistema solare e consentendoci di riportare a casa, con l’ausilio di precisi calcoli matematici, anche l’equipaggio dell’Apollo 13.
Ebbene si, il problema dei tre corpi non solo riguarda sistemi formati da tre o più corpi celesti, ma anche sistemi composti da pianeti, stelle e sonde spaziali.
Quindi esiste una soluzione al problema dei tre corpi? La risposta è “si e no”, perché esistono delle soluzioni molto complesse che risolvono il problema grazie a sequenze infinite di numeri. Nel 1915, infatti, il matematico finlandese Karl Sundman arrivo alla prima soluzione teorica del problema dei tre corpi che, però, non contraddiceva affatto Poincaré.
Quella di Sundman, infatti, è una soluzione che si basa su una serie infinita di numeri impossibile da gestire. L’avvento dei computer e della loro capacità di svolgere calcoli complessi con estrema rapidità, ha permesso di sfruttare al massimo le intuizioni di Sundman, anche se la parola magica per la soluzione del problema dei tre corpi è “approssimazione”, ovvero metodi per arrivare a soluzioni numeriche che ci consentano di capire, in maniera approssimata per l’appunto, cosa succede ai tre corpi.
Il problema dei tre corpi ristretto e le approssimazioni che salvano Matt Damon
Queste approssimazioni ci portano al cosiddetto modello del problema dei tre corpi ristretto, ovvero situazioni in cui al noto e facilmente risolvibile problema dei due corpi si aggiungono piccole variazioni.
È il caso in cui, per esempio, avendo due corpi se ne aggiunge un altro con una massa praticamente trascurabile a livello gravitazionale. Ecco, dunque, che è possibile prevedere con esattezza (sempre frutto di approssimazioni via via più precise) il comportamento di un sistema formato per esempi dalla Terra, dalla Luna e da una sonda o una navicella spaziale.
La potenza via via crescente dei computer e le simulazioni sempre più affidabili del problema degli n-corpi (con n che è un numero maggiore di 2) hanno permesso ai ricercatori di studiare una vasta gamma di scenari, dall’evoluzione delle orbite planetarie nel sistema solare fino alla formazione delle galassie. In molti casi, la nostra comprensione di questi fenomeni deriva da simulazioni al computer basate sulle soluzioni approssimate del problema dei tre corpi. Tuttavia, anche con tutta la moderna tecnologia computazionale, alcune configurazioni del problema dei tre corpi rimangono ancora sfide insormontabili.
Sebbene possa sembrare un puro esercizio accademico, arrivato sotto le luci della ribalta grazie alla serie TV di Netflix, il problema dei tre corpi ha numerose applicazioni pratiche in vari campi scientifici. Per esempio, come già detto, è fondamentale per la navigazione spaziale, per la gestione delle orbite satellitari, per la pianificazione di missioni interplanetarie e per poter salvare Matt Damon abbandonato su Marte.